¡Felices paseos!:
- Por aristas de sólidos, siguiendo a “una hormiga exploradora”
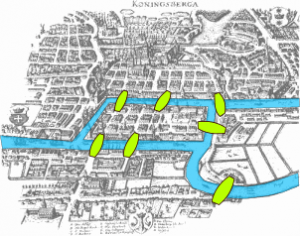
- Por los puentes de ciudades fluviales -¡Konisberg!-.
- Por las puertas de una vieja mansión.
- Compartiendo el vértigo de los esquiadores de slalon.
- En turismo rural, por pueblos casi perdidos.
- Con el dominó.
- Con una baraja.
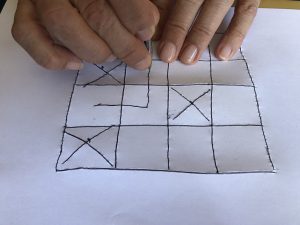
- Por los cuadros de una cuadrícula…
La presentación un tanto lúdica de algunas situaciones no creo necesite justificación. Es una forma de trabajar en el aula que no estorba -que «no me estorba», y pienso que a mis alumnos tampoco- y que reviste la Matemática de amabilidad. (Reviste: no disfraza; Amabilidad: no trivialidad, ni frivolidad.)
Los problemas de itinerarios trabajados en pequeño grupo o grupo coloquial son ocasión para ejercicios de expresión en los distintos lenguajes didácticos y consiguiente traducción permanente:
- Permite -siempre es posible la manipulación de objetos. Que deberán tener un diseño inclusivo, accesible para el estudiante DV.
- Describir oralmente situaciones gráficas y manipulativas, estáticas o dinámicas.
El habla o lengua natural sigue siendo el vehículo de comunicación en el aula más inmediato y claro en un curriculum donde la descripción y la expresión oral parecen haber quedado relegadas a los relatos de sucesos pasados.
- Siempre conveniente en Matemáticas, y más con alumnos ciegos y deficientes visuales -que no es raro presenten carencias representativas-. Con variedades:
- representaciones geométricas o esquemáticas –ordinarias-;
- la representación mediante deformaciones topológicas; y
- los diagramas de segmentos (grafos de Euler).
- A los que vendría a sumarse un género de representación proyectiva de tres a dos dimensiones, sustentada en deformaciones homotópicas.
Sin dificultad para el estudiante DV, gracias a la “lámina de caucho”.
- Reducir estados y acciones físico-geométricas a expresión simbólico-matemática, en un afán de economía de tiempo y esfuerzo. A nuestros estudiantes DV les bastará el braille.
Gracias a Euler, por su Teoría de Grafos, por su Topología.
Por aristas de sólidos, tras “una hormiga exploradora”: hormiga con salakof

Por los puentes de ciudades fluviales -¡Konisberg!-: Konisber o Kaliningrado,
Por las salas de viejas mansiones: mansión-palacete en medio del bosque o campo

Compartiendo el vértigo de los esquiadores de slalon: esquiador cruzando una puerta de slalon

En turismo rural, por pueblos casi perdidos: tartana con turistas,

Con el dominó: fichas de dominó

Con una baraja: 9 ó 10 naipes

Por los cuadros de una cuadrícula